Matemática – Estatística

1. (Epcar (Afa) 2017) As notas de oito alunos numa prova de matemática foram escritas pelo professor numa tabela como a que segue:

Sabe-se que a média aritmética dessas notas é 8,2.

Considerando as notas dos oito alunos, é correto afirmar que a nota do aluno G é;

a) igual à moda.
b) inferior a 9,8.
c) superior à mediana.
d) inferior à média aritmética das outras sete notas.

2. (Eear 2017) A tabela seguinte informa a quantidade de pessoas que compraram ingressos antecipados de um determinado show, cujos preços eram modificados semanalmente.

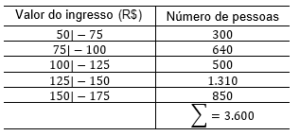
O percentual de pessoas que adquiriram o ingresso por menos de R$ 125,00 foi;

a) 40%
b) 45%
c) 50%
d) 55%

3. (Ufpr 2016) Em um grupo de 6 pessoas, a média das idades é 17 anos, a mediana é 16,5 anos e a moda é 16 anos. Se uma pessoa de 24 anos se juntar ao grupo, a média e a mediana das idades do grupo passarão a ser, respectivamente:

a) 17 anos e 17 anos.
b) 18 anos e 17 anos.
c) 18 anos e 16,5 anos.
d) 20,5 anos e 16,5 anos.
e) 20,5 anos e 20,25 anos.

4. (G1 – cp2 2016) Observe com atenção o quadro a seguir.

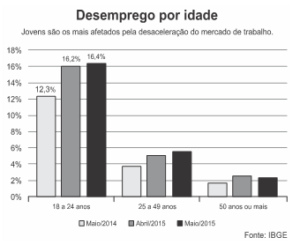
IBGE: desemprego sobe mais entre jovens de 18 a 24 anos, chegando a 16,4%

O aumento do desemprego em maio foi maior entre os jovens, segundo o IBGE (Instituto Brasileiro de Geografia e Estatística). (Fonte: www.uol.com.br. Adaptado. Acessado em: 25/06/2015.)

No último censo realizado em 2010, o IBGE estimava a população de jovens entre 18 e 24 anos em torno de 24 milhões. Supondo que o número não tenha se alterado e tomando-o por base, pode-se dizer que o número de desempregados nessa faixa, 18 a 24 anos, aumentou, no último ano em, aproximadamente;

a) 500 mil.
b) 1 milhão.
c) 1 milhão e meio.
d) 2 milhões.

5. (Ufrgs 2016) O gráfico a seguir representa a população economicamente ativa de homens e mulheres no Brasil de 2003 a 2015.

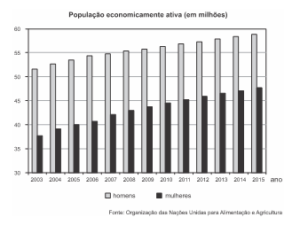
Com base nos dados do gráfico, é correto afirmar que,

a) no ano de 2009, a população economicamente ativa de mulheres era cerca de 50% da população economicamente ativa de homens.
b) de 2003 a 2015, em termos percentuais, a população economicamente ativa de homens cresceu mais do que a de mulheres.
c) em relação a 2005, a população economicamente ativa de mulheres em 2011 cresceu cerca de 5%.
d) de 2003 a 2015, em termos percentuais, a população economicamente ativa de mulheres cresceu mais do que a de homens.
e) em relação a 2007, a população economicamente ativa de homens em 2015 cresceu cerca de 3%.

6. (Ueg 2016) Os números de casos registrados de acidentes domésticos em uma determinada cidade nos últimos cinco anos foram: 100, 88, 112, 94 e 106. O desvio padrão desses valores é aproximadamente;

a) 3,6
b) 7,2
c) 8,5
d) 9,0
e) 10,0

7. (Epcar (Afa) 2016) Um cursinho de inglês avaliou uma turma completa sendo que parte dos alunos fez a avaliação cujo resultado está indicado no gráfico abaixo.

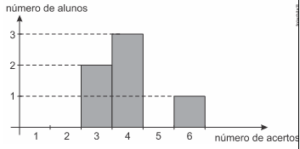
Os demais alunos fizeram a avaliação B e todos tiveram 4 acertos. Assim, o desvio padrão obtido a partir do gráfico acima ficou reduzido à metade ao ser apurado o resultado da turma inteira.

Essa turma do cursinho de inglês tem;

a) mais de 23 alunos.
b) menos de 20 alunos.
c) 21 alunos.
d) 22 alunos.

8. (Eear 2016) Ao calcular a média aritmética das notas dos Testes Físicos (TF) de suas três turmas, um professor de Educação Física anotou os seguintes valores:

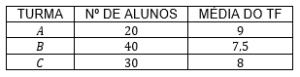
9. (Upe-ssa 2 2016) Preocupada com o hábito de leitura na escola onde trabalha, uma bibliotecária aplicou uma pesquisa, num grupo de 200 estudantes escolhidos de forma aleatória, sobre a quantidade de livros que cada aluno havia solicitado por empréstimo no primeiro semestre de 2015. Os dados coletados na pesquisa estão apresentados na tabela a seguir:

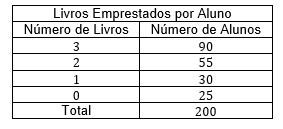
Para esses dados, a média, a moda e a mediana são respectivamente:

a) 1,50; 2,00; 3,00
b) 1,50; 3,50; 2,00
c) 1,50; 3,00; 3,00
d) 2,05; 3,00; 2,00
e) 2,05; 3,00; 3,00

10. (Eear 2016) A distribuição de frequência abaixo refere-se à exportação de soja realizada por uma Cooperativa no mês de abril.

Com base nos dados apresentados, a mediana da distribuição pertence à;

a) 2ª classe
b) 3ª classe
c) 4ª classe
d) 5ª classe

11. (G1 – ifsp 2016) O gráfico abaixo apresenta informações sobre a participação dos três únicos vendedores de uma pequena corretora no valor total de vendas de seguros, no segundo quadrimestre de 2015.

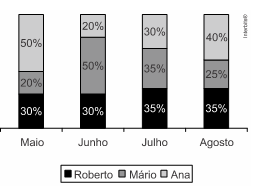
Com base nas informações apresentadas, assinale a alternativa que contém uma afirmação correta.

a) Não houve mês em que dois vendedores tiveram o mesmo valor de venda.
b) O valor das vendas de Roberto, em junho, e o valor das vendas de Ana, em julho, foram necessariamente iguais.
c) O valor das vendas de Mário, em agosto, foi necessariamente menor que o valor das vendas de Ana, em julho.
d) No mês de maio, o valor das vendas de Ana necessariamente correspondeu a 250% do valor das vendas de Mário.
e) Em todos os quatro meses do segundo trimestre de 2015, os valores em vendas da corretora foram iguais.

Gabarito:

Resposta da questão 1:
[C]

Calculando:

(6,5+10+8+9,4+8+6,4+x+7,4)/8=8,2
6,5+10+8+9,4+8+6,4+x+7,4=65,6→x=9,9
Moda=8
Mediana=(8+8)/2=8
Média das outras 7 notas=(6,5+10+8+9,4+8+6,4+7,4)/7=7,96

Assim, a única alternativa correta é a letra C.

Resposta da questão 2:
[A]

Tem-se que a resposta é dada por

(300+640+500)/3.600⋅100%=40%.

Resposta da questão 3:
[B]

Considere os termos: x_1,x_2,x_3,x_4,x_5,x_6, termos de sequencia.

Temos:

Média aritmética vale isto é:
(x_1+x_2+x_3+x_4+x_5+x_6)/6=17⇒x_1+x_2+x_3+x_4+x_5+x_6=102

Mediana valendo
____, ____, 16,  17, ____, ____⇒(x_3+x_4)/2=16,5

Moda valendo

____, 16,  16,  17, ____, ____, 24

Portanto, teremos:
Média aritmética⇒(x_1+x_2+x_3+x_4+x_5+x_6+24)/7⇒(102+24)/7⇒18

Mediana⇒x_1+x_2+x_3+x_4+x_5+x_6+24⇒Mediana=x_4=17

Resposta da questão 4:
[B]

(16,4-12,3)/100⋅24.000.000=984.000

Ou seja, aproximadamente 1 milhão de desempregados.

Resposta da questão 5:
[D]

[A] Falsa, pois

[B] Falsa.
Taxa de crescimento dos homens: (58-52)/52=0,12=12%
Taxa de crescimento das mulheres: (47-37)/37=0,27=27%

[C] Falsa.
(45-40)/40=0,125=12,5%

[D] Verdadeira. Veja justificativa do item [B].

[E] Falsa.
(58-54)/54=0,08=8%

Resposta da questão 6:
[C]

Calculando a média aritmética, temos:
¯x=(100+88+112+94+106)/5=100

E depois o desvio padrão:
√σ=√(((100-100)^2+(100-88)^2+(100-112)^2+(100-94)^2+(100-106)^2)/5)=√72≈8,5

Resposta da questão 7:
[A]

1ª Solução: Considere a tabela, referente aos resultados no exame A.

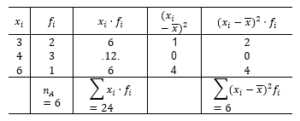
A média no exame foi

¯x_A=(∑▒〖x_i⋅f_i 〗)/n_A =24/6=4.

Logo, sabendo que todos os alunos tiveram 4 acertos no exame B, segue que a média da turma, ¯x, também é 4.

Se é o desvio padrão no exame então;

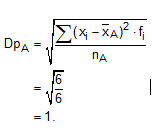
Chamando de o número total de alunos, e sabendo que o desvio padrão da turma, Dp_T, é igual à metade do desvio padrão no exame A, temos

Dp_T^2=(∑▒〖(x_j-¯x )^2⋅f_j 〗)/n⇔(1/2)^2=6/n
⇒n=24.

2ª Solução: Considere a tabela, referente aos resultados no exame A.

Daí, segue que o desvio padrão da turma é igual a 1/2 e, portanto, se é o número de alunos da turma, então

(1/2)^2=1/n⋅(16n+6-((4n)^2)/n)⇔1/4=6/n⇔n=24.

3ª Solução: Considere a tabela, referente aos resultados no exame A.

A média no exame A foi

x_A=(∑▒〖x_i⋅f_i 〗)/n_A =24/6=4.

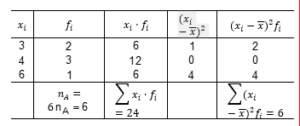
O desvio padrão no exame é dado por ;

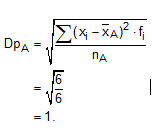
Logo, o desvio padrão da turma é igual a Dp_T=1/2.

Por outro lado, sabendo que todos os alunos que fizeram o exame B tiveram 4 acertos, é imediato que a

média no exame B foi ¯x_B=4, e o desvio padrão Dp_B=0.

Em consequência, sendo n_B o número de alunos que fizeram o exame B e ¯x_A=¯x_B=¯x, temos;

Dp_T^2=(n_A⋅Dp_A^2+n_B⋅Dp_B^2)/(n_A+n_B )⇔(1/2)^2=(6⋅1^2+n_B⋅0^2)/n
⇔1/4=6/n
⇔n=24.

Resposta da questão 8:
[A]

Faremos a média aritmética ponderada (M) das médias de cada turma.
M=(20⋅9+40⋅7,5+30⋅8)/(20+40+30)=720/90=8

Resposta da questão 9:
[D]

Considere a tabela.

Tem-se que a média é igual a 410/200=2,05.
Sendo 3 o valor mais frequente, podemos concluir que a moda vale 3. Ademais, como o número de observações é igual a 200, segue que a mediana é igual à média aritmética das observações de ordem 100 e ordem 101, isto é, (2+2)/2=2.

Resposta da questão 10:
[C]

Determinando o intervalo de classe onde se encontra a mediana, temos:
(∑▒f_i )/2=30/2=15 a primeira frequência acumulada maior que 15 é a da 4ª classe.

Portanto, a mediana dos dados se encontra na 4ª classe.

Resposta da questão 11:

[D]

[A] Falsa. Em julho Roberto e Mário apresentaram percentuais iguais sobre o total. Logo, tiveram o mesmo valor de venda.
[B] Falsa. Não há informação sobre o total de vendas em junho e julho.
[C] Falsa. Por motivo análogo ao da alternativa [B].
[D] Verdadeira. De fato, temos (50%)/(20%)⋅100%=250%.
[E] Falsa. O fato das colunas terem a mesma altura não implica em valores totais em vendas iguais.