Geometria analítica – Cônicas

1. (Espcex (Aman) 2016). Considere as afirmações:

I. Uma elipse tem como focos os pontos F_1 (-3, 0), F_2 (3, 0) e a medida do eixo maior é Sua equação é x^2/16+y^2/7=1.
II. Os focos de uma hipérbole são F_1 (-10, 0), F_2 (10, 0) e sua excentricidade é 5/3. Sua equação é 16x^2-9y^2=576.
III. A parábola 8x=-y^2+6y-9 tem como vértice o ponto V(3, 0).

Com base nessas afirmações, assinale a alternativa correta.

a) Todas as afirmações são falsas.
b) Apenas as afirmações I e III são falsas.
c) Apenas as afirmações I e II são verdadeiras.
d) Todas as afirmações são verdadeiras.
e) Apenas a afirmação III é verdadeira.

2. (Mackenzie 2016) Com relação às equações das elipses 25x^2+16y^2+150x+256y-351=0 e 16x^2+25y^2-96x-200y+144=0, podemos afirmar que;

a) as elipses têm centros coincidentes.
b) as elipses têm a mesma distância focal.
c) as elipses têm a mesma excentricidade.
d) as elipses têm focos sobre o eixo das abscissas.
e) o eixo maior de uma delas é o dobro do eixo menor da outra.

3. (Epcar (Afa) 2016) Analise as proporções abaixo e escreva V para a(s) verdadeira(s) e F para a(s) falsa(s).

I. ( ) A distância entre o vértice e o foco da parábola y^2+4x-4=0 é igual a 1 unidade de comprimento.
II. ( ) Numa hipérbole equilátera, as assíntotas são perpendiculares entre si.
III. ( ) A equação 2x^2+y^2-4x-4y+4=0 representa uma elipse que tem um dos focos no ponto P (1 , 4)

A sequência correta é;

a) F – F – V
b) V – F – V
c) F – V – F
d) V – V – F

4. (G1 – ifce 2016) A expressão x^2+y^2-2x-4y+ 4=0 descreve a equação de um(a),

a) hipérbole.
b) parábola.
c) elipse.
d) círculo.
e) reta.

5. (Ime 2015) Determine o produto dos valores máximo e mínimo de y que satisfazem às inequações dadas para algum valor de x.

2x^2-12x+10≤5y≤10-2x
a) -3,2
b) -1,6
c) 0
d) 1,6
e) 3,2

6. (Espcex (Aman) 2015) Uma reta t passa pelo ponto A(-3,0) e é tangente à parábola de equação x=”3″ “y” ^2 no ponto P.

Assinale a alternativa que apresenta uma solução correta de acordo com essas informações. a) t:x-10y+3=0 e P(27,3)

b) t:2x-15y+6=0 e P(12,2)
c) t:2x-15y+6=0 e P(12,-2)
d) t:y=0 e P(0,0)
e) t:x+6y+3=0 e P(3,-1)

7. (Unifor 2014) Uma bola é jogada dentro de uma cesta cuja superfície é obtida girando a parábola y=x^2 em torno do eixo y. O centro da bola ocupa um ponto de altura y=3. O raio da bola é:

a) √11
b) √11/2
c) √11/3
d) √11/4
e) √11/5

8. (Fgv 2014) No plano cartesiano, há dois pontos R e S pertencentes à parábola de equação e que estão alinhados com os pontos A(0,3) e B(4,0).

A soma das abscissas dos pontos R e S é:

a) -0,45
b) -0,55
c) -0,65
d) -0,75
e) -0,85

9. (Ime 2014) Uma elipse cujo centro encontra-se na origem e cujos eixos são paralelos ao sistema de eixos cartesianos possui comprimento da semi-distância focal igual a √3 e excentricidade igual a √3/2. Considere que os pontos A, B, C e D representam as interseções da elipse com as retas de equações y=x e y=-x. A área do quadrilátero ABCD é;

a) 8
b) 16
c) 16/3
d) 16/5
e) 16/7

10. (Espcex (Aman) 2014) Sobre a curva 9×2 + 25y2 – 36x + 50y – 164 = 0, assinale a alternativa correta.

a) Seu centro é (– 2,1).
b) A medida do seu eixo maior é 25.
c) A medida do seu eixo menor é 9.
d) A distância focal é 4.
e) Sua excentricidade é 0,8.

Gabarito:

Resposta da questão 1:
[C]

[I] Verdadeira.
x^2/a^2 +y^2/b^2 =1

Admitindo os focos (c, 0) e (-c, 0), temos:
e

Portanto, a equação da elipse será:
x^2/16+y^2/7=1.

[II] Verdadeira.
c=10
5/3=10/a⇒a=6
10^2=6^2+b^2⇒b=8

Portanto, a equação da hipérbole será dada por:
x^2/6^2 -y^2/8^2 =1⇒16x^2-9y^2=576

[III] Falsa.
8x=-y^2+6y-9
x=-((y-3)^2)/8
Portanto, o vértice é o ponto (0, 3).

Resposta da questão 2:
[C]

Completando os quadrados, vem

25x^2+16y^2+150x+256y-351=0⇔25(x+3)^2+16(y+8)^2=1.600
⇔((x+3)^2)/64+((y+8)^2)/100=1

e

16x^2+25y^2-96x-200y+144=0⇔16(x+3)^2+25(y-4)^2=400
⇔((x+3)^2)/25+((y-4)^2)/16=1.

[A] Falsa. Os centros das elipses são os pontos (-3, -8) e (-3, 4).
[B] Falsa. Com relação à elipse ((x+3)^2)/64+((y+8)^2)/100=1, temos a=10 e b=8. Logo, pela relação fundamental, segue que c=6 e, portanto, 2c=12.
Por outro lado, na elipse ((x+3)^2)/25+((y-4)^2)/16=1, temos a^’=5 e b^’=4. Assim, vem c^’=3 e, portanto, 2c^’=6.
[C] Verdadeira. Com efeito, pois e=6/10=3/5=e^’.
[D] Falsa. Basta observar que o eixo maior da elipse ((x+3)^2)/64+((y+8)^2)/100=1 é paralelo ao eixo das ordenadas.
[E] Falsa. O eixo maior da elipse ((x+3)^2)/64+((y+8)^2)/100=1 mede 2a=20, enquanto que o eixo menor da elipse ((x+3)^2)/25+((y-4)^2)/16=1 mede
2b^’=8.

Resposta da questão 3:
[D]

Analisando as proposições:

[I] VERDADEIRA. Podemos reescrever a equação da parábola dada:
y^2+4x-4=0→x=-1/4 y^2+1

Assim, temos que quando x=0, y=±2, e quando y=0, x=1. Com isso pode-se construir um gráfico e identificar que trata-se de uma parábola com concavidade voltada para a esquerda, que corta o eixo y nos pontos +2 e -2, cujo vértice tem coordenadas (0, 1). Conclui-se também que eixo de simetria da parábola é o próprio eixo x (x=0).
O foco de uma parábola fica sempre sobre o eixo de simetria (portanto, nesse caso, x=0), com y=k+p onde k será a coordenada y do vértice e p=1/4a.

Assim, a coordenada y do foco será:
k=1
p=1/(4⋅(-1)/4)=-1
y=k+1→y=1-1 → y=0

Logo, as coordenadas do foco serão (0, 0) e sua distância até o vértice é igual a 1. A alternativa é verdadeira.

[II] VERDADEIRA. A proposição é verdadeira pois esta é justamente a definição de hipérbole equilátera: ter as assíntotas perpendiculares entre si.

[III] FALSA. Podemos reescrever a equação dada de modo a facilitar as conclusões:
(2x^2-4x)+(y^2-4y+4)=0→(x-1)^2/1+(y-2)^2/2=1

Comparando esta equação com a equação geral de uma elipse, pode-se concluir que a equação dada trata-se de uma elipse de centro (1 , 2), semi-eixo menor b=1 e semi-eixo maior a=√2. A elipse pode ser representada graficamente como na figura a seguir:

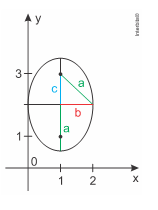
Sabendo que a^2=b^2+c^2, então c=1. Daí pode-se deduzir que os focos da elipse serão (1, 3) e (1, 1). A proposição é falsa.

Resposta da questão 4:
[D]

x^2+y^2-2x-4y+ 4=0⇔x^2-2x+1+y^2-4y+4=-4+5⇔(x-1)^2+(y-2)^2=1

Temos então a equação de uma circunferência com centro no ponto (1, 2) e raio 1.

A melhor opção, entre as apresentadas, é a [D], ou seja, um círculo.

Resposta da questão 5:
[A]

Temos duas regiões a serem considerada.
5y≥2x^2-12x+10
5y≤10-2x

A região que satisfaz as duas inequações simultaneamente está representada no gráfico abaixo.

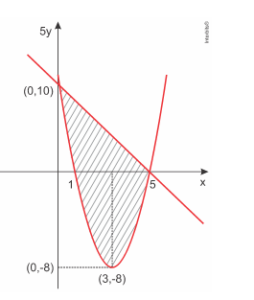
Portanto, -8≤5x≤10⇒-1,6≤y≤2.
O produto dos valores máximo e mínimo de y é -1,6⋅2=-3,2.

Resposta da questão 6:
[E]

Seja (t) a reta tangente à parábola de equação x=”3″ “y” ^2.

(t)y=mx+n, como o ponto A( -3,0) pertence a (t) concluímos que n=3m e a equação da reta t passa a ser escrita por y=mx+3m.

Substituindo y=mx+3m na equação da parábola, temos:

x=3⋅(mx+3m)^2
x=3⋅(m^2 x^2+6m^2 x+9m^2)
x=3m^2 x^2+18m^2 x+27m^2
3m^2 x^2+(18m^2-1)x+27m^2=0

Para que a reta seja tangente à parábola o discriminante deverá ser igual à zero.

Δ=0
(18m^2-1)^2-324m^4=0
-36m^2+1=0⇒m=1/6  ou  m=(-1)/6

Se m=1/6, temos x-6y+3=0.
Se m=(-1)/6, temos x+6y+3=0.

Fazendo m=(-1)/6, temos:
x^2-6x-9=0⇒x=3 ou y=-1.

Resposta da questão 7:
[B]

Seja o raio da bola.

A equação da circunferência de centro (0, 3), tangente à parábola y=x^2, é dada por

x^2+(y-3)^2=r^2. Daí, segue que

x^2+(x^2-3)^2=r^2⇔x^4-5x^2+9-r^2=0.

Tomando x^2=t, obtemos t^2-5t+9-r^2=0. Assim, como o discriminante dessa equação deve ser igual a zero, vem

(-5)^2-4⋅1⋅(9-r^2)=0⇔r^2=11/4 ⇒r=√11/2.

Resposta da questão 9:
[D]

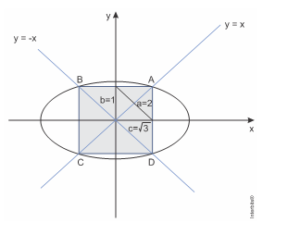
Excentricidade: c/a=√3/2⇒√3/a=√3/2⇒a=2

a^2=b^2+c^2⇒2^2+〖√3〗^2⇒b=1

Equação da Elipse: x^2/4+y^2/1=1

Determinando os pontos de encontro através do sistema, temos:
{(x^2/4+y^2=1@@y=±x)┤⇒A(2/√5,2/√5),” B” (-2/√5,2/√5),” C” (-2/√5,-2/√5)” e D” (2/√5,-2/√5)

O lado do quadrado será dado por: AD=2/√5-(-2/√5)=4/√5
Logo, sua área será A=(4/√5)^2=16/5.

Resposta da questão 10:
[E]

9×2 + 25y2 – 36x + 50y – 164 = 0

9(x2 – 4x + 4) + 25(y2+ 2y + 1) = 164 + 36 + 25

9(x – 2)2 + 25(y + 1)2 = 225

((x-2)^2)/25+((y+1)^2)/9=1

Equação de uma elipse com centro no ponto (2, –1), eixo maior igual a 10, eixo menor igual a 6, distância focal igual a 8 e excentricidade e = 4/5 = 0,8.
Portanto, a afirmação [E] é a verdadeira.